The Deuce: Rolling 3 dice and getting all the same is not 1/6... It's 6/216, or 1/36.*

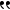Let's calculate the probability of rolling **three of a kind** using **three dice** and **four dice** to determine how much the odds increase.

### **Case 1: Rolling 3 Dice**
We need exactly **three** dice to show the same number.

1. Pick a number (1-6) that will be the triplet → Probability = \( \frac{1}{6} \).
2. The first die can be any number → Probability = \(1\).
3. The second die must match the first → Probability = \( \frac{1}{6} \).
4. The third die must also match → Probability = \( \frac{1}{6} \).

Thus, the probability of rolling three of a kind exactly is:
\[
6 \times \left(\frac{1}{6} \times \frac{1}{6}\right) = \frac{6}{36} = \frac{1}{6} \approx 16.67\%
\]

### **Case 2: Rolling 4 Dice**
We need at least **three** of the four dice to show the same number.

#### **Scenario 1: Exactly 3 Matching, 1 Different**
1. Pick the matching number (1-6) → \( \frac{1}{6} \).
2. Choose which three dice will match (ways to choose 3 out of 4) → \( \binom{4}{3} = 4 \).
3. The three matching dice each roll that number → \( \left(\frac{1}{6}\right)^2 \).
4. The fourth die rolls a different number (5 choices) → \( \frac{5}{6} \).

\[
6 \times 4 \times \left(\frac{1}{6} \times \frac{1}{6}\right) \times \frac{5}{6} = \frac{120}{1296} \approx 9.26\%
\]

#### **Scenario 2: All 4 Matching**
1. Pick the number → \( \frac{1}{6} \).
2. All four dice must roll that number → \( \left(\frac{1}{6}\right)^3 \).

\[
6 \times \left(\frac{1}{6} \times \frac{1}{6} \times \frac{1}{6}\right) = \frac{6}{216} = \frac{1}{36} \approx 2.78\%
\]

### **Total Probability (Rolling 4 Dice)**
Adding both scenarios together:

\[
9.26\% + 2.78\% = 12.04\% \text{ (extra chance with 4th die)}
\]

\[
16.67\% + 12.04\% = 28.7\%
\]

### **Odds Increase**
\[
\frac{28.7\%}{16.67\%} \approx 1.72
\]

So, rolling **4 dice instead of 3 increases your odds by about 72%** of rolling three of a kind.